Dynamic Mechanical Analysis (DMA) is used to determine the mechanical properties of viscoelastic materials by subjecting them to cyclic loading as a function of temperature, time and frequency.
The SDTA861 is characterised by a wide frequency range of 0.001 Hz to 1000 Hz, a temperature range of -150 °C to 500 °C and a force range of 0.01 to 12 N.
Different loads are possible. The mode chosen depends not only on the problem but also on the type of sample:
Shear: The advantage of this measurement mode is that samples can be measured from viscous to very hard. It is suitable for elastomers, thermoplastics and thermosets.
Tension: This type of loading is suitable for films, fibres and thin rods.
Compression: This type of measurement allows conclusions to be drawn about soft materials such as elastomers.
3-point bending: This mode is particularly suitable for very rigid samples such as composites, even below the glass transition temperature.
Single cantilever bending: This geometry is suitable for samples that expand or contract during measurement, such as thermoplastics.
Dual cantilever bending: This mode is particularly suitable for samples that tend to flex excessively under high pre-stress.
Applications
The DMA can be used for a wide range of applications in virtually all sectors of industry.
The table below shows that the DMA is mainly used for measuring glass transition temperature, studying curing reactions of thermosets and polymerisation of elastomers for process optimisation or for studying damping. Modulus values can also be determined.
Examples illustrating the various application areas of the DMA SDTA861
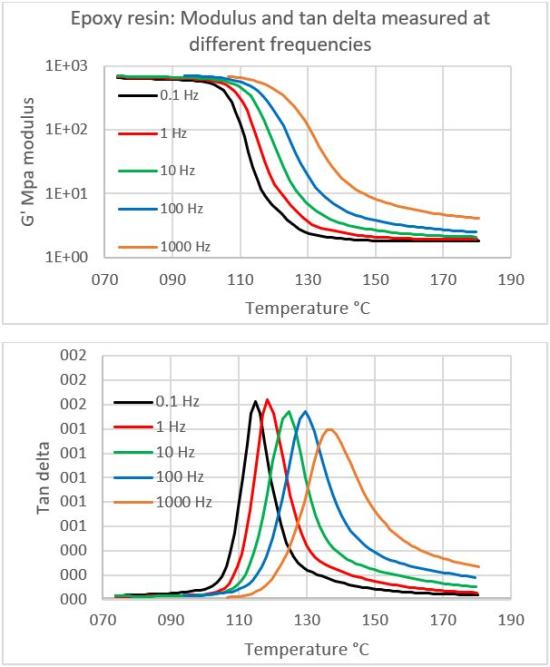
Modulus and delta tangent measurement of an epoxy resin cured at different frequencies
The modulus and glass transition temperature of an epoxy resin or composite material can be measured as a function of temperature by the DMA. The delta tangent moves to higher temperatures as the frequency increases. The decrease in modulus during the glass transition is accompanied by a peak in the delta tangent.
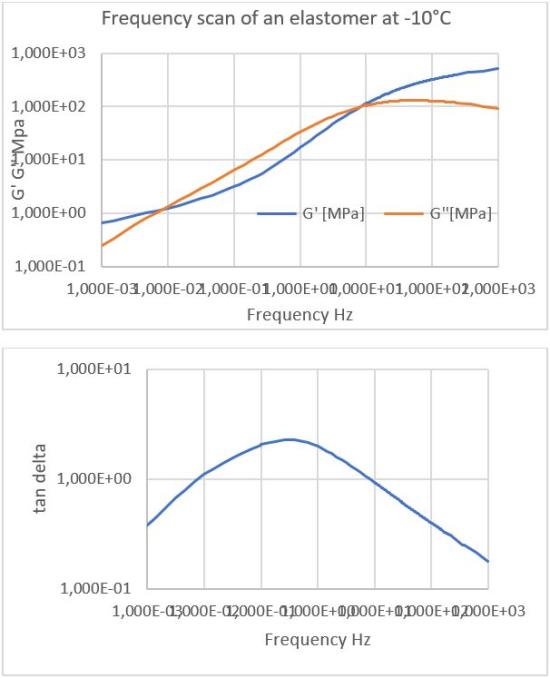
Frequency scan of an elastomer
In practice, materials are loaded over a wide frequency range, with the properties changing with frequency. In this case, the modulus increases and the loss factor reaches a maximum of 0.32 Hz.
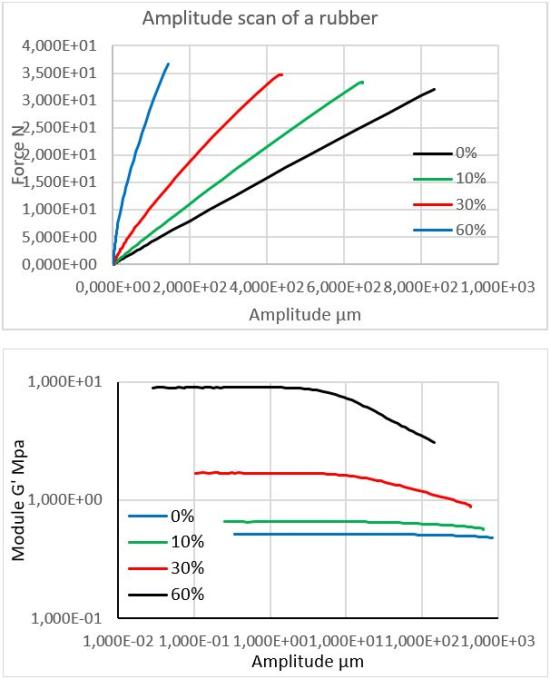
Displacement amplitude scan of a rubber
The modulus of filled polymers increases with the loading rate but decreases with increasing strain amplitude.
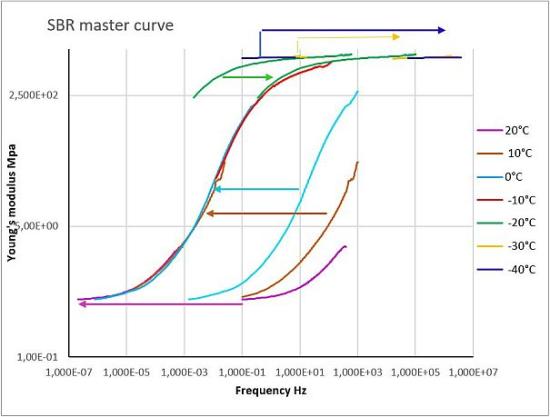
Master curve technique
Measuring the viscoelastic properties of materials at high frequencies is necessary in many industrial applications such as tyre performance and safety prediction, noise and vibration reduction in mechanical engineering, acoustic design of vehicles and industrial processing machines.
Viscoelastic behaviour is frequency and temperature dependent. There is an equivalence between frequency and temperature related behaviour during transition processes. This equivalence is called TTS (Time-Temperature Superposition) and forms the theoretical basis for the master curve technique which allows the prediction of polymer behaviour outside the range accessible during a test. This is because:
- High frequencies are equivalent to low temperatures. The sample is in a glassy state and therefore has a high modulus.
- Low frequencies are equivalent to high temperatures. The sample is in a rubbery state and therefore has a low modulus.
The master curve technique extends the approximately four decades of experimentally accessible frequencies to about 20. The individual isothermal scans are shifted to a chosen reference temperature.
More information on the Mettler Toledo DMA SDTA861 in our Sirris Test Labs.
The DMA SDTA861 is one of the 4 pieces of equipment in our new thermal analysis chain. This chain also includes a Flash DSC 2+, a TMA SDTA2+ and a DSC.